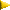 Quelques notions sur la résistance des matériaux
Quelques notions sur la résistance des matériaux
|
Il ne s'agit pas de faire ici un cours sur la résistance des matériaux mais seulement d'exposer quelques notions élémentaires pour en comprendre un minimum. Tout d'abord, il faut savoir que la déformation d'un objet implique que la distance de certains couples de points de cet objet varie. Ceci est une propriété géométrique (négation d'une isométrie). D'une façon plus simple on dira qu'une partie de cet objet subit une compression et une autre partie un étirement Un exemple d'école est celui d'une poutre à section rectangulaire qui subit une charge
Sur ce dessin on constate que sous l'effet de la charge matérialisée par la flèche la poutre qui repose en D et C subit une déformation qui entraine une diminution de la distance AB et une augmentation de CD La fibre AB ou plutôt la couche en surface AB subit une compression et la couche du dessous DC subit un étirement (On a fait l'hypothèse de conserver des angles droits en A,B,C,D ) Les couches internes subissent égalent des compressions ou des étirements mais leur amplitude est moindre que celle des couches de surface. Il existe au milieu une couche qui n'est ni comprimée, ni étirée. Elle est appelée couche (ou fibre) neutre. Elle sépare la partie comprimée de la partie étirée On constate donc que la rigidité d'un objet est liée à la capacité du matériau à s'étirer et à se comprimer. De plus la forme géométrique influe fortement sur la rigidité de l'objet. En effet, pour un même affaissement de la poutre (flèche) la différence des longueurs de l'arc AB et de l'arc CD est d'autant plus grande que l'épaisseur (AD) de la poutre est importante. Ainsi la forme géométrique peut être telle qu'une petite déformation entraine localement de gros étirements ( ou compressions) Ceux qui ont une certaine expérience de la construction plastique des canoës ou des kayaks savent bien qu'il faut avoir une plus grande épaisseur (ou même des renforts de rigidité) sur les grandes surfaces planes, que sur les surfaces fortement incurvées Remarque: Dans la construction dite "sandwich", on utilise pleinement ceci en essayant d'augmenter fortement l'épaisseur AD en remplaçant les couches internes (qui travaillent très peu pendant une flexion) par un matériau léger Une petite expérience à faire: 1) Si vous prener une feuille de papier vous constater qu'elle n'est pratiquement pas élastique et poutant elle n'a aucune rigidité. Ceci est du à sa très faible épaisseur 2) Si vous prener une plaque caoutchouc elle ne sera pas rigide bien qu'épaisse car il s'agit d'un matériau très élastique (faites un dessin sur les deux faces et vous verrez mieux comment une face s'étire et l'autre se compresse) 3) Si vous coller sur les deux faces de la plaque en caoutchouc une feuille de papier vous aurez un ensemble relativement rigide (ne pas utiliser un papier trop fin qui risque de se froisser). Si l'épaisseur de notre poutre, mis sous flexion, est très importante la déformation sera alors quelque peu différente du cas précédent. Le dessin ci-dessous illustre la situation
Vu la grande épaisseur, la flexion doit entraîner des variations de longueurs considérables de DC et de AB, ce qui entraine des contraintes de force très importantes et les différentes couches internes entre les couches de surface AB et CD coulissent les unes sur les autres (à l'image d'un cahier que l'on plie et dont les feuilles glissent alors les unes sur les autres). Dans le cas des composites stratifiés, cette situation où les couches glissent sur les autres est appelée délaminage. Les pratiquants de l'eau vive connaissent bien ce genre de dégat sur leur bateau après une rencontre avec un rocher. Un choc avec flexion sur une structure sandwich entraine souvent le même résultat. Dans les laboratoires, on utilise souvent ce type de flexion sur des éprouvettes très épaisses, pour mesurer la capacité d'un composite de résister au délaminage. En conclusion, les matériaux intéressants pour la rigidité sont ceux qui opposent une très grande résistance à l'étirement et à la compression. Cette aptitude d'un corps à s'opposer à son étirement est mesurée par un nombre appelé module d'élasticité. D'une façon plus précise, la force F qu'il faut appliquer à un échantillon cylindrique pour obtenit un allongement dl de sa longueur est donné par F = e.s.dl / l où e représente le module d'élasticité, s la section du cylindre et l sa longueur (à une constance multiplicative près pour tenir compte des unités de mesure). En écrivant F/s =e.dl/l, on contate que e est un coefficient multiplicateur entre une pression F/s et un poucentage d'allongement dl/l Pour simplifier la suite de l'étude on supposera les unités choisies de sorte à avoir s=1.
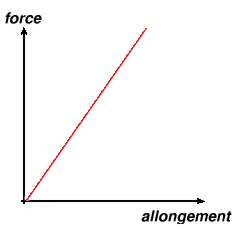
En posant x = dl/l et y= F/s on a donc y = e.x et cette relation se représentera graphiquement par une droite passant par l'origine de coefficient directeur e ( Rappelons que le coefficient directeur nous indique la pente de la droite. Dans les livres scolaires, l'équation de la droite est souvent notée par y = ax et a est le coefficient directeur) Donc pour un matériau rigide cette droite est fortement inclinée Un corps quelconque ne peut indéfiniment s'allonger. Quand un certain poucentage d'allongement est obtenu sur notre cylindre de test, il se casse en deux morceaux. Comme pour le module d'élasticité, le pourcentage d'allongement à la rupture est aussi une caractéristique de chaque corps. En analysant la formule précédente, on contate que la résistance d'un matériau est donnée par le produit de son module par son allongement à la rupture.
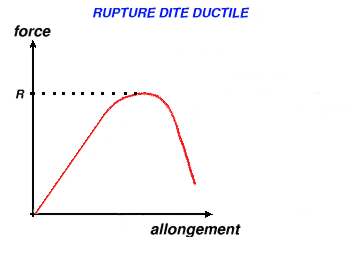
(Cette étude faite sur les allongements peut aussi s'appliquer à la compression et on peut définir le module d'élasticité en compression.) Certains corps ne se rompent pas aussi brutalement qu'indiqué ci-dessus. Ils se cassent en quelque sorte comme un corps pâteux.. La rupture est dite ductile par opposition à la rupture brutale qui est dite fragile (un matériau à rupture fragile peut être mécaniquement très résitant)
Dans ce type de rupture, on contate qu'il existe un premier allongement en dessous duquel il n'y a aucune altération du matériau. Si l'étirementt se pousuit sans atteindre l'allongement à la rupture, il se produit des déformations irréversibles dans le corps qui ne possède plus ses qualités d'origine. (penser à l'étirement d'une pâte à modeler) Il arrive souvent qu'un corps soit percuté par un autre. Il se pose alors le problème de l'absorbtion d'énergie.
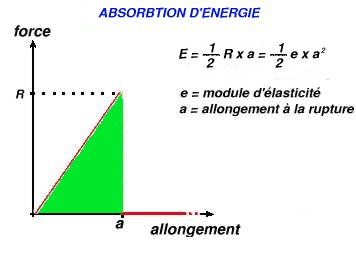
Rappelons que l'énergie mécanique est égal au produit scalaire de la force et du déplacement. Si la force varie pendant le déplacement il faut utiliser la valeur moyenne de celle-ci qui est de (½)R pour une rupture fragile. En multipliant ce nombre par l'allongement a on aura l'énergie maximum absorbable sans dépasser l'allongement à la rupture. Cette énergie correspond donc à l'aire du triangle représentée en couleur verte Dans le cas d'une rupture ductile le calcul de l'énergie absorbable ne peut plus se faire aussi simplement
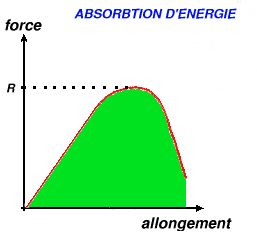
La valeur moyenne de la force n'est plus égale à la moitié de R comme précédement. Il faut avoir recours au calcul intégral pour obtenir cette énergie. Elle correspond à l'aire de la zone représentée en couleur verte Les paragraphes qui vont suivre utiliseront ces notions que nous venons de voir |
 Au départ ABCD est un rectangle donc AB
=CD
Au départ ABCD est un rectangle donc AB
=CD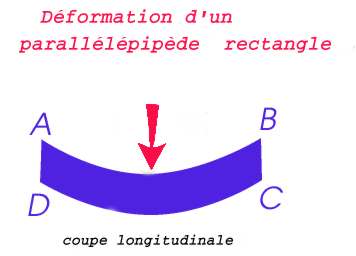 On contate que les angles en A, B,C et D ne sont
plus droits et les longueurs des arcs AB et DC sont égales. Une telle
situation se produit lorsqu'on veut réaliser
On contate que les angles en A, B,C et D ne sont
plus droits et les longueurs des arcs AB et DC sont égales. Une telle
situation se produit lorsqu'on veut réaliser